NEHRU JARPULA

---

1. A point object is placed at (-40,7) cm in front of a concave mirror 
of focal length 5 cm having its pole at the origin (0,0). Assuming 
the principal axis to be along x-axis, find the position of the 
image formed?

::Answer:: 

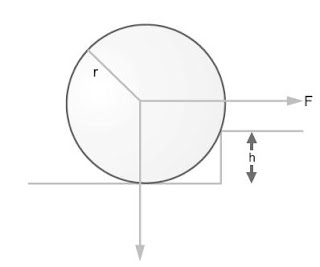
2.A wheel of radius r and weight W is to be raised over an obstacle of height h by a horizontal force F applied to the centre. Find the minimum value of F.(As shown in fig).

::Answer::

3. A heavy wheel of radius 20 cm and weight 10 kg is to be dragged over a step of height 10 cm, by a horizontal force F applied at the centre of the wheel. Find the minimum value of F.

::Answer::
F = w √(h(2r-h))/(r-h)
= 10 √(10(2(20)-10))/(20-10) = √300
F = 10√3 kg wt


4. A coin is kept at a distance of 10 cm from the centre of a circular turn table. If the coefficient of static friction between the table and the coin is 0.8 find the frequency of rotation of the disc at which the coin will just begin to slip?

::Answer::

Condition for just slipping, the required condition is
mrω^2 = µmg
r x 4π^2 n^2 =µg
n^2= (µg)/(r4π^2 )
= (0.8x9.8)/(0.1x4x9.8 ) = 2
n=√2 rps or
n = 1.414x60 =84. 84 rpm

5. A ball is dropped on the floor from a height 10 m. It rebounds to a height of 2.5 m. If the ball is in contact with floor for 0.01 sec, what is the average acceleration during the contact?

::Answer::

Velocity with which ball hits the ground
u = √(2 gh) = √(2 (9.8)(10))
u = 14 m/s
Velocity v with which the ball rebounds
v = √(2 gh) = √(2 (9.8)(2.5))
v = 7 m/s
∆v = v – u
∆v = 7 – (-14) = 21 m/s
a = (∆v )/(∆t ) = (21 )/(0.01 )
a = 2100 m /s^2
6. A satellite is launched into a circular orbit of radius “R’ around the earth while a second satellite is launched into an orbit of radius 1.02 R. The percentage difference in the time periods of the two satellites is:

::Answer::

The centripetal force (Fc) acting on the satellite revolving round the Earth along the orbit having radius R is given by
Fc=mω^2R
The gravitational force (Fg) acting on the satellite will provide the required centripetal force.
Fg =GmM/R2
Now Fc = Fg
=>mω^2R=GmM/R^2
=>(2π/T)^2R=GM/R^2
=>T^2=(4π^2/GM)R^3.......(1)
Now differentiating (1) w.r to R we get
⇒2TdT=(4π^2/GM)⋅3R^2dR........(2)
Dividing (2) by (1) we get
2dT/T=3dR/R
⇒dT/T=3/2(dR/R)......(3)
Now by the problem change in radius of the satellite is
dR=1.02R−R=0.02R
Inserting this value of dR=0.02R in equation (3) we get the percentage change in time period of second satellite w.r to the time period of first satellite.
% change in time period
=dT/T×100%=3/2(0.02R/R)×100%

=3%

---